RNN常见结构

1. 介绍

深度学习中，虽然CNN除了被经常用来进行图像相关的任务外，也可以作为一种特征提取的方法用在NLP任务中。但是在NLP任务中，更多的我们还是使用RNN模型，本文就简单介绍几种常用的RNN结构。

2. 基本RNN

不同于在CNN模型中，网络的状态只决定于输入。在RNN中，最明显的一个特征就是它还决定于上一个时刻的状态，因此RNN经常被用来处理序列问题，被用在序列性质非常明显的NLP任务上。

基本的RNN结构如下：

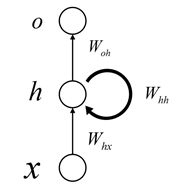
它跟CNN和DNN区别最大的地方就在于这些前馈神经网络是个有向无环图的模型(DAG)，而在RNN中是至少包含一个环的，在时间上进行展开我们可以更明显的看到这种特性：

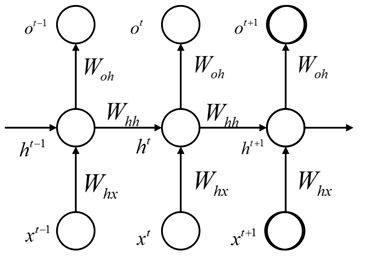
公式可以表示为：

$$\begin{aligned}& h^t = tanh(W_{hx}x^t + W_{hh}h^{t-1}+b_h) \\\\ &o^t = softmax(W_{oh}h^t + b_o) \end{aligned}$$

其中$x^t$是t时刻的输入，在NLP任务中，通常代表一句话中第t位置处的字。隐藏层的状态h不光决定于当前的输入，还决定于前一个时间t-1的状态，通过矩阵$W_{hh}$联系t-1的状态和当前状态，通过$W_{hx}$联系当前输入$x^t$和当前状态，这里的激活函数通常可以使用tanh函数。对于t时刻的输出通常可以使用一个softmax回归，参数矩阵为$W_{oh}$。

3. RNN的反向传播 -- BPTT

可以看到，类似于CNN在不同位置上共享卷积矩阵的参数，RNN在不同时刻t是共享参数的。对于不同时刻t，使用的是同样的$W_{hh}, W_{oh}$。对于RNN的反向传播有自己的一套算法BPTT，BP是反向传播，TT是Through Time。在介绍BPTT之前，先回忆一下在DNN中的反向传播。DNN的结构如下：

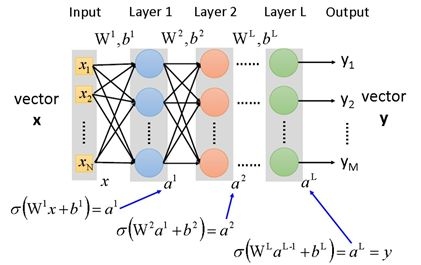
可以看到，前向过程的公式为：

$$\begin{aligned} &z^1 = W^1x+b^1 \\\\ & a^1 = \sigma(z^1) \\\\ &... \\\\&z^L = W^La^{L-1}+b^{L-1}\\\\&a^L = \sigma(z^L) \end{aligned}$$

方向传播的话先定义一个中间变量:

$$\delta^l = \frac{\partial{C}}{\partial{z^l}}$$

代表损失函数C关于第l层的未激活输出$z^l$的偏导数，然后对于任意一层的参数$W^l$的偏导数为：

$$\frac{\partial{C}}{\partial{W^l}} = \frac{\partial{C}}{\partial{z^l}}\frac{\partial{z^l}}{\partial{w^l}}$$

其中$\frac{\partial{z^l}}{\partial{w^l}}$为$a^{l-1}$，这个在一次前向过程中已经全部求得，反向传播要做的事就是通过一次反向过程求得所有的$\frac{\partial{C}}{\partial{z^l}}$，也就是所有层的$\delta{l}$。

通过求导的链式法则：

$$\delta^{l-1} = \frac{\partial{C}}{\partial{z^{l-1}}} = \frac{\partial{a^{l-1}}}{\partial{z^{l-1}}}\frac{\partial{z^l}}{\partial{a^{l-1}}}\frac{\partial{C}}{\partial{z^l}}=\sigma'(z^{l-1})\cdot(W^l)^T\delta^l$$

于是可以得到类似于前向过程的反向过程公式：

$$\begin{aligned} &&\delta^L = \sigma'(z^L)\cdot \triangledown C(a^L)\\\\ && \delta^{L-1} = \sigma'(z^{L-1})\cdot(W^L)^T\delta^L\end{aligned}$$

可以看到，前向过程是从第1层一直到第L层进行计算，而这里是从第L层到第1层计算每层的$\delta^l$，所以这种算法被称为反向传播算法。

讲完了DNN的情况，这里再来理解RNN的情况。RNN的特殊在于时间t引入。将RNN沿时间进行展开：

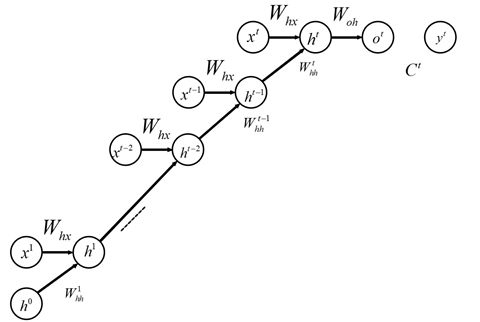
可以发现，RNN展开后的结构和DNN的结构原理上是一样的。只是在DNN中，链接发生在相邻的隐藏层上面。而在RNN中，链接发生在相邻时间上。

然后DNN每一层的参数是不一样的，而在RNN中一个序列样本下，不同时间上的参数是一致的。在这种情况下，如果我们最后考虑的损失函数只和最末尾的t时刻的输出$o^t$相关的话（情感分析，文本分类等都属于这种情况），在进行参数$\beta$的更新时需要考虑每个时刻t上的损失函数对$\beta$的梯度之和，即：

$$\frac{\partial{C^t}}{\partial{\beta}} = \sum_k \frac{\partial{C^t}}{\partial{\beta^k}}$$

这里的$\beta^k$是参数在时间k上的状态，可以看作是DNN中的第k层的参数，于是利用反向传播可以求出每个时刻k的偏导数。但是实际上不同时刻k的参数$\beta$是一个统一的参数，因此需要进行累加作为对参数$\beta$总的偏导数。

如果我们考虑的损失函数和每个时刻的输出都有关（序列标注等属于这种情况），即$C = f(C^1, C^2, ..., C^{t-1}, C^t)$，则有：

$$\frac{\partial{C}}{\partial{\beta}} = \sum_{k=1}^t\frac{\partial{C^k}}{\partial{\beta}}\frac{\partial C}{\partial{C^k}}$$

对于其中的每一时刻$\frac{\partial C^k}{\partial \beta}$，都需要考虑k时刻以前所有的对$\beta$的偏导数的和：

$$\frac{\partial C^k}{\partial \beta}= \sum_{j=1}^k \frac{\partial C^k}{\partial \beta^j}$$

于是得到，关于$\beta$的总的导数为：

$$\frac{\partial{C}}{\partial{\beta}} = \sum_{k=1}^t\sum_{j=1}^k \frac{\partial C^k}{\partial \beta^j}\frac{\partial C}{\partial{C^k}}$$

4. RNN的梯度爆炸/消失

可以看到RNN的BPTT算法与DNN的BP算法非常相似，只是前者发生在时间上，后者发生在隐藏层上。那么对于时间跨度很长的情况，BPTT就很可能会发生梯度爆炸或者梯度消失的情况。

激活函数：

像DNN一样，如果激活函数是$\sigma$函数或者tanh函数，进行反向传播的时候很容易就会导致梯度很小，产生梯度消失的问题。

参数$W_{hh}$：

不同于DNN中每层的参数是不一样的，RNN中的参数$W_{hh}$每个时刻是一个参数，所以在进行反向传播的时候会进行$W_{hh}$的累乘。

当$W_{hh}$为对角阵时，我们就有结论：

当对角线元素小于1，则其幂次会趋近于0，进而导致梯度消失
当对角线元素大雨1，则其幂次会趋近于无穷大，进而导致梯度爆炸

当$W_{hh}$不是对角阵时，对矩阵进行随机初始化。观察累乘后的分布如下：

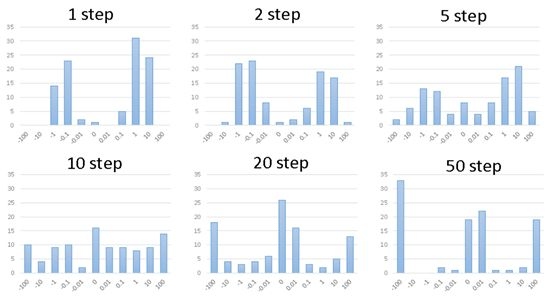
可以看到，经过一定次数的相乘以后，大部分的数值都是趋近于绝对值大的数，要么趋近于0。这就分别对应了梯度爆炸和梯度消失的情况。

理论上，$W_{hh}$是个方阵，简化问题，假设它是可以进行对角化的，那么可以分解为$Q\sum Q^{-1}$，其中的$\sum$也是对角矩阵，累乘的话同样会发生上面讨论的对角阵相乘的情况。

处理梯度消失/爆炸的方法

梯度消失：

传统的使用RELU等激活函数的方法有效，但是存在更好的RNN架构直接就可以解决这样的问题，比如下文中要介绍的LSTM，GRU等。

梯度爆炸：

通常还是使用Gradient Clipping，在梯度大于一个阈值的时候，进行动态的放缩，将它限制在一定范围内。

5. BRNN

BRNN就是Bi-directional RNN，双向的RNN。前面的讨论都是单向的，从前到后，双向就是多了一层，从后到前：

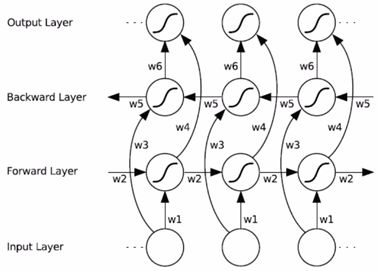
对于每一个时刻t，它隐藏层的状态不光决定于前向层经过该时刻带来的状态h1，还决定于后向层经过该时刻带来的状态h2，然后进行链接[h1, h2]得到的就是在时刻t上的状态。两层可以分别保留各自的参数$W_{hh}$，虽然使用不同的维度在理论上是可以的，但是实际上通常前向层和反向层保持维度一致。

这种模型带来的好处是显而易见的，它不光能够考虑当前时间受前面时间的影响，还能考虑受后面时间的影响，看几个简单的例子来感受一下：

在命名实体识别中，“我们爱吃红烧肉”，根据前向层很容易根据爱吃推断红烧肉是一道菜名，但是在“红烧肉很好吃”中，如果只根据前向，就比较难判断了，这个时候如果加上后向层，就可以根据很好吃判断它前面的字段红烧肉是菜名了。
在情感分析中，“这个公园好美啊，尽管有一点拥挤”，如果只看前向可能会比较倾向于把这个句子判断为负情感，但是如果加上反向的特征的话，就更容易判断争取，识别为正情感。

当然上面的例子只是简要说明一下双向的好处，实际的算法肯定不是这么浅显直观的计算的。

既然BRNN只是在RNN的基础上反向加了一层，本质是一样的，只是训练的时候考虑两层的参数，这里就不再重复介绍了。

6. LSTM

前面的讨论表明理论上RNN在考虑前后文联系的时候可以发挥不错的作用，尤其是当相关信息的位置间隔比较短的时候：

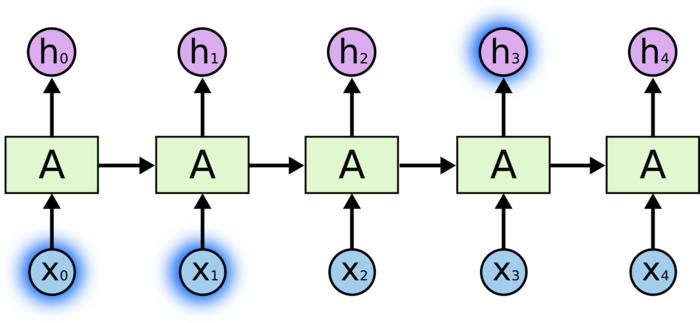
但是根据前一小节的讨论，当相关信息的位置间隔越来越长的时候，由于存在梯度消失的问题，在基础RNN上进行这样的参数学习非常困难的。

LSTM，long short term网络的出现就解决了这样的问题，它可以非常轻松的学习到序列中的长期依赖信息。

LSTM通常指的是里面的RNN网络中的LSTM Cell，类似于下图：

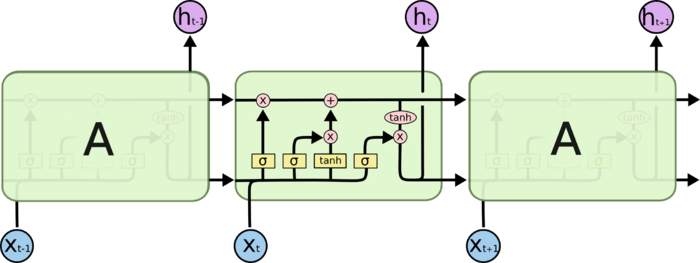
普通的RNN Cell，并没有中间那么复杂的链接，基本就是一个隐藏层+激活函数（通常使用tanh），而在在上图的LSTM Cell中有四个进行交互的层，后面可以看到这些是LSTM中的各种功能的门函数。

6.1 LSTM核心思想

LSTM中很重要的信息载体就是其每时刻的细胞状态，它会沿着水平线上传播。它在整个链上传播的过程中，会进行一些简单的线性操作。

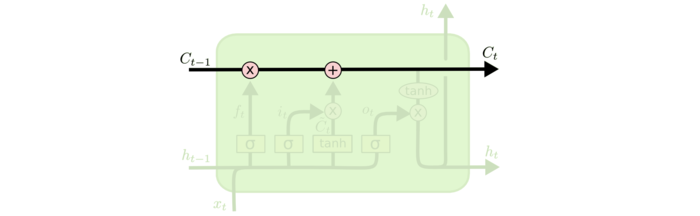
这些线性操作会使得信息可以增加或者减少，而决定信息是如何增加或者减少的话就要依靠LSTM中定义的各种门函数。每个门可以理解为一个开关，0表示不通过，1表示通过，0到1之间的数表示部分通过，因此门函数使用sigmoid神经网络层代替，在sigmoid输出一个值后进行pointwise的操作：

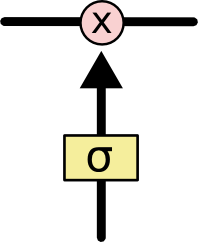
6.2 LSTM中的三个门

遗忘门

在LSTM的第一步中要决定过去的信息需要遗忘多少，保留多少，遗忘们就起到这样的作用。它通过一个参数矩阵$W_f$（f代表forget），作用于上一个隐藏层的状态$h_{t-1}$和当前输入$x_t$，然后通过sigmoid函数得到一个[0, 1]的数：

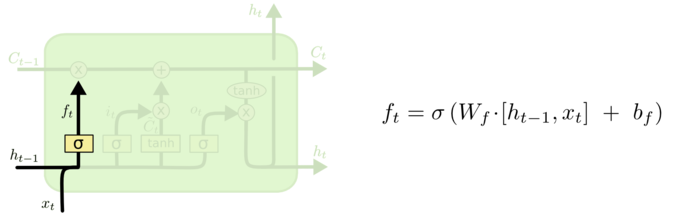
回到具体的语言模型情况，考虑当前的细胞状态$C_{t-1}$包含当前主语的性别，我们想要预测合适的代词。如果当前的输入$x_t$包含新的主语，这个时候就要通过遗忘门来忘掉旧的主语。

输入门

知道了要忘掉哪些信息后，就要决定记住哪些新的输入信息了。

首先新的信息依靠一个参数矩阵$W_C$和tanh激活函数，然后哪些信息需要记忆依靠的是类似遗忘门的sigmoid神经层计算的一个输入门函数。

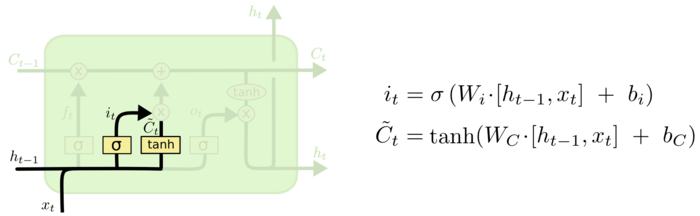
其中$i_t$是输入门层，决定要更新什么值，就是要记住哪些新的信息，然后$\tilde{C}_t$是候选的新的状态。

然后依靠遗忘门和输入门的线性组合就可以得到新的细胞状态了：

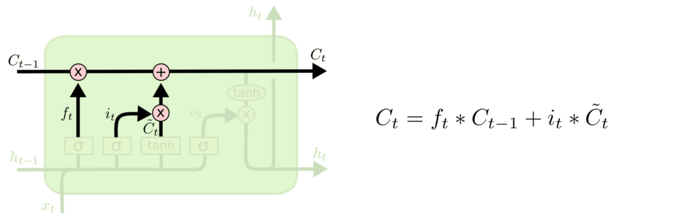
可以看到新的细胞状态有两个部分，一个是有旧的细胞状态带来的，一个是有新的输入信息带来的。

语言模型的例子里，我们希望模型新的细胞状态能记住新的主语的性别。

输出门

在得到了新的细胞状态$C_t$后，就能够直接通过激活函数(tanh)得到我们的输出了。不过这里我们仍然要一个门控制输出哪些信息，同样使用sigmoid神经层：

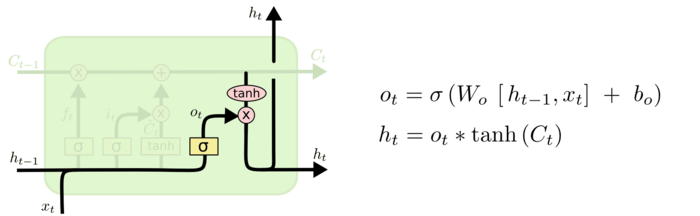
在语言模型的例子里，有可能是看到一个代词就选择输出一个跟动词有关的信息。

LSTM结构的个人理解

通过上面LSTM结构的解析，我们可以看到网络的输出和计算三个门的值所使用的都是$h_t$。于是可以这样理解，在LSTM网络沿着时间传播的过程中，细胞状态$C_t$时刻保存着最重要的信息。然后上一时刻的网络输出$h_{t-1}$和当前的网络输入$x_t$通过对应的矩阵计算得到三个门的值。输入门和遗忘门负责合并过去细胞状态和当前新信息，输出门负责控制对更新后的细胞状态的选择性输出。当前时刻的输出又被用来进行下一时刻三个门的计算。

6.3 LSTM的变体

上面的LSTM是标准的LSTM结构，下面讨论几个变体。

peephole connection

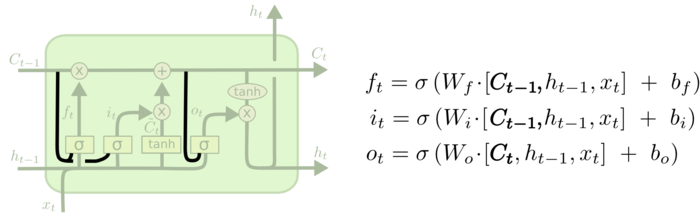
从上面的结构可以看出peephole connection就是让门的计算也同样受细胞状态的影响：遗忘门和输入门受上一时刻细胞状态$C_{t-1}$的影响，计算输出门时当前的时刻的细胞状态$C_t$已经计算好了，于是收到$C_t$的影响。从公式中也可以很容易看出三个门计算中对于细胞状态的引入。

当然三个peephole connection可以有选择的添加，并非一定要三个一起加入。

coupled forget gate and input gate

不同一开始遗忘门和输入门分别计算，coupled就是只计算遗忘门$f_t$，然后输入门就是$1-f_t$。

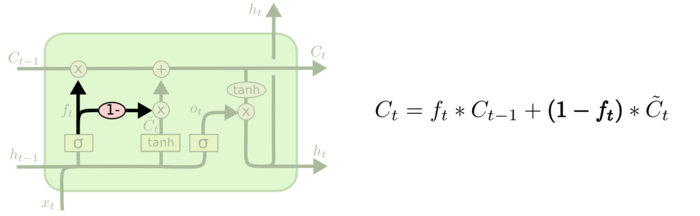
在这种情况下，当遗忘门确定的时候，输入门也同时被确定。当我们要保留旧细胞状态的时候($f_t = 1$)，新信息就完全不会被加入。当我们要遗忘旧细胞状态的时候($f_t = 0$)，新的细胞状态完全由新信息决定。

6.4 LSTM与梯度消失

在描述LSTM的一开始，就说了它可以处理在长期记忆上产生的梯度消失问题，它具体是怎们做的呢？

先看一下LSTM反向传播时$\delta^k = \frac{\partial C^t}{\partial c^k}$是怎么传播的：

$$\delta^{k-1} = \frac{\partial C^t}{\partial c^{k-1}} = \frac{\partial C^t}{\partial c^k} \frac{\partial c^k}{\partial c^{k-1}} = \delta^k \frac{\partial c^k}{\partial c^{k-1}}$$

根据LSTM的公式$c^t = f^t \cdot c^{t-1} + i^t \cdot g^t$ 可以的到上式可以转变为：

$$\delta^{k-1} = \delta^k (f^t + ...)$$

上面的省略号是一些无关部分，不影响我们的分析。可以看到，当$f^t = 1$时，省略号那部分无论多小，梯度都是可以很容易反向传播的。此时，即使是学习长期记忆也不会发生梯度消失问题。当$f^t=0$时，上一时刻的信号不影响到当前时刻，$f^t$在这里控制着梯度传递到前一时刻的衰减程度，和它在遗忘门上的功能是一致的。

7. GRU

GRU和LSTM有着一定的相似性，算是一个简化版本的LSTM。它将遗忘门和输入门合并为更新门，因此只有两个门。而且它没有细胞状态$C_t$的流动，只保留隐藏状态$H_t$。

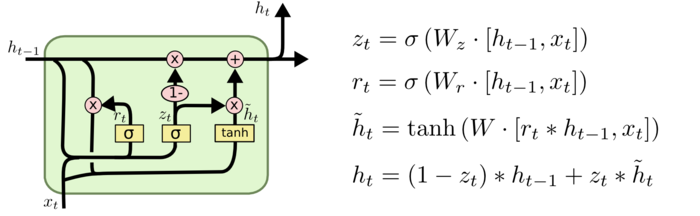
上图中的$r_t$是reset gate 重置门，它负责对过去的隐藏状态$h_{t-1}$进行取舍，以用来计算新的候选隐藏状态$\tilde{h_t}$。不同于LSTM中，门函数是作用于tanh激活的计算结果，这里的重置门直接作用于计算过程中的$h_{t-1}，$可以看到如果$r_t=0$，在计算$\tilde{h_t}$时，完全受当前输入$x_t$的影响。

$z_t$是更新门，它负责选择$h_{t-1}$在新的输出$h_t$中所要记住的信息，注意到这里旧的信息和新的信息的合并是coupled。

8. 结构的选择

上面讲了LSTM，GRU及其很多变体，Greff, et al.(2015)给出了一些流行变体的比较，结论是它们基本一致。其它的一些论文比较，也通常只是发现在具体任务上，某些结构可能会优于某些结构，但是总的来说，并没有哪个结构一定是最好的。

至于LSTM和GRU的选择，通常效果也差不多，不过GRU有更少的参数，相对来说容易训练，过拟合的情况也会好很多，更适用于训练数据较少的情形。

9. 结论

目前看来RNN架构的发展是要弱于CNN的，不过LSTM和GRU解决了RNN中长期依赖的问题，在RNN中取得了巨大的成功。由于RNN常用的结构少于CNN，这里就用一篇文章总结了一下常见RNN的结构。不过论模型的难度的话，无论是理论还是应用，RNN都是要难于CNN的。

LSTM的出现算得上是RNN中一个突破性的进展，接下来可能attention机制是一个很重要的研究热点。自己今后也要多多关注和学习这一方面的内容。

参考资料

[1] Understanding Deep Learning in One Day - 李宏毅

[2] 当我们在谈论数据挖掘 - 余文毅

[3] Understanding LSTM Networks - Christopher Olah

[4] LSTM: A Search Space Odyssey - Klaus Greff, et al

[5] Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures - Alex Graves, et al

RNN常见结构

1. 介绍

2. 基本RNN

3. RNN的反向传播 -- BPTT